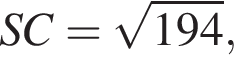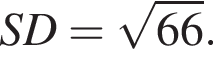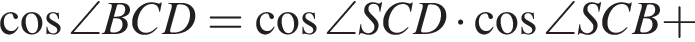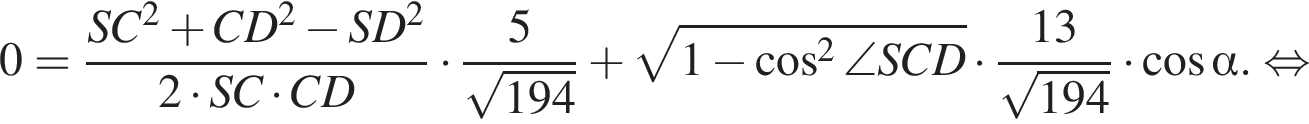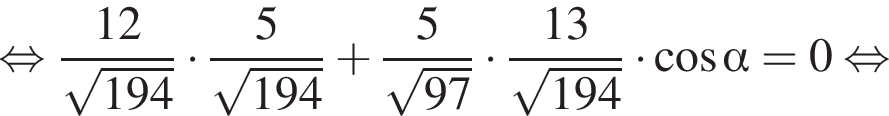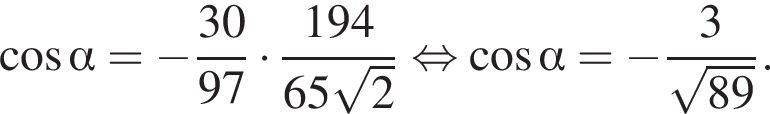На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между B и D равно ![]() то ближе других к точке с координатой 1,01 расположена точка:
то ближе других к точке с координатой 1,01 расположена точка:
Централизованное тестирование по математике, 2018
В треугольнике ABC известно, что 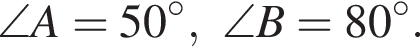 Укажите номер верного утверждения для сторон треугольника.
Укажите номер верного утверждения для сторон треугольника.
Две окружности с центрами A и B касаются в точке M. Найдите длину отрезка CN, если
 и диаметр большей окружности на 35 больше радиуса меньшей окружности.
и диаметр большей окружности на 35 больше радиуса меньшей окружности.
На рисунке две прямые пересекаются в точке О. Если
 то угол BOC равен:
то угол BOC равен:
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 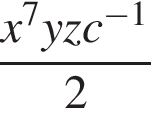 | б) | в)  | г) 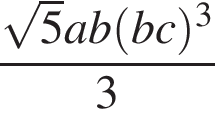 | д) |
На рисунке приведен график изменения скорости тела в зависимости от времени. Запишите закон движения тела на промежутке от 40 мин до 80 мин.
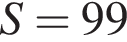

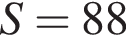
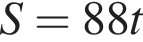

Вычислите 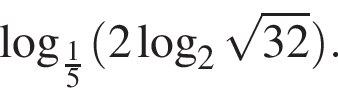
Последовательность задана формулой n-го члена 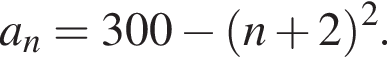 Вычислите
Вычислите 
Решением системы неравенств 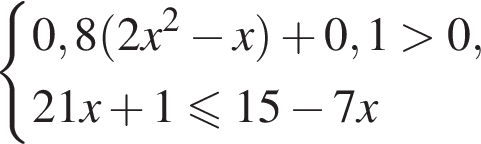 является:
является:
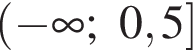
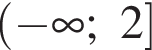


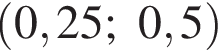
Значение выражения 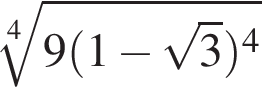 равно:
равно:
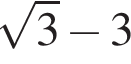
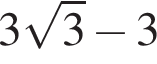
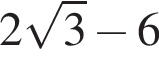
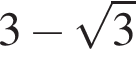
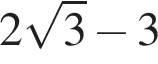
Укажите уравнение, равносильное уравнению 
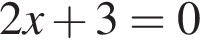
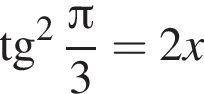
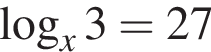
Площадь параллелограмма равна ![]() его стороны равны 6 и 2. Найдите большую диагональ параллелограмма.
его стороны равны 6 и 2. Найдите большую диагональ параллелограмма.
Найдите значение выражения 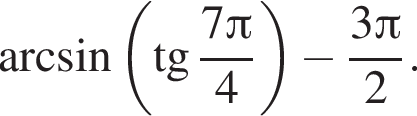
Составьте уравнение для определения площади заштрихованной фигуры.
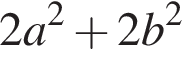
Окружность задана уравнением 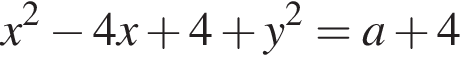 и проходит через вершину параболы
и проходит через вершину параболы 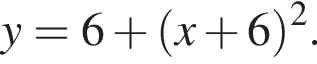 Найдите радиус этой окружности.
Найдите радиус этой окружности.
Площадь боковой поверхности цилиндра равна ![]() а его объем равен
а его объем равен ![]() Найдите высоту цилиндра.
Найдите высоту цилиндра.
Найдите сумму корней уравнения 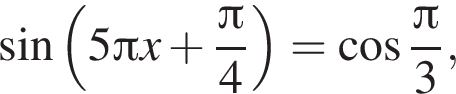 принадлежащих промежутку
принадлежащих промежутку 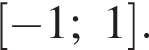
В правильной треугольной призме ребра основания равны 16, а высота равна 9. Найдите площадь сечения призмы плоскостью MNP, если
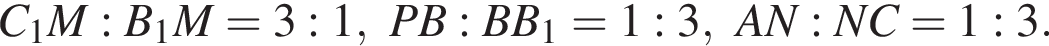

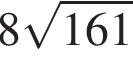

Выберите все верные утверждения, являющиеся свойствами нечетной функции ![]() определённой на
определённой на  и заданной формулой
и заданной формулой 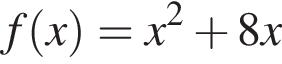 при
при ![]()
1. Функция имеет три нуля.
2. Функция убывает на промежутке [5; 7].
3. Максимум функции равен 16.
4. Минимальное значение функции равно −16.
5. 
6. Функция принимает отрицательные значения при 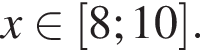
7. График функции симметричен относительно оси абсцисс.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Внутренний угол правильного многоугольника равен 135°. Выберите все верные утверждения для данного многоугольника.
1. Многоугольник является восьмиугольником.
2. В многоугольнике 20 диагоналей.
3. Если сторона многоугольника равна 1, то радиус вписанной окружности равен 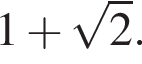
4. Площадь многоугольника со стороной a можно вычислить по формуле 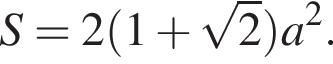
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Цену товара увеличили на 20%, а через неделю — еще на p%. В результате первоначальная цена товара увеличилась на 56%. Найдите значение p.
Найдите произведение корней (корень, если он единственный) уравнения 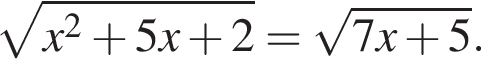
Найдите сумму всех натуральных чисел a, для которых выполняется равенство 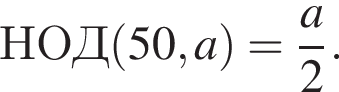
Найдите произведение наименьшего решения на количество решений уравнения 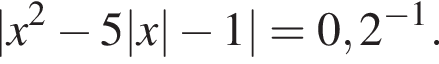
Найдите количество целых решений неравенства 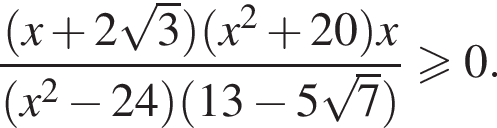
Найдите сумму целых решений неравенства 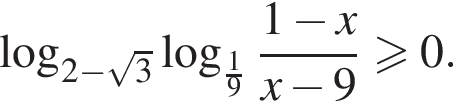
Если ![]() и
и ![]() — корни уравнения
— корни уравнения  то значение
то значение ![]() равно ... .
равно ... .
В остроугольном треугольнике ABC проведены высоты BE и CD. Найдите длину CB, если 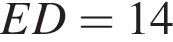 и радиус окружности, описанной вокруг AED равен 25. Укажите в ответе величину 12CB.
и радиус окружности, описанной вокруг AED равен 25. Укажите в ответе величину 12CB.
Двое рабочих выполняют некоторую работу. Сначала первый работал ![]() часть времени, за которое второй выполняет всю работу. Затем второй работал
часть времени, за которое второй выполняет всю работу. Затем второй работал ![]() часть времени, за которое первый закончил бы оставшуюся работу. Оба они выполнили только
часть времени, за которое первый закончил бы оставшуюся работу. Оба они выполнили только ![]() всей работы. Сколько часов потребуется рабочему с меньшей производительностью для выполнения этой работы, если известно, что при совместной работе они сделают ее за 4 ч?
всей работы. Сколько часов потребуется рабочему с меньшей производительностью для выполнения этой работы, если известно, что при совместной работе они сделают ее за 4 ч?
На стороне AB параллелограмма ABCD отмечена точка O так, что 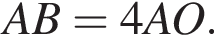 К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 5. Найдите значение выражения
К плоскости ABCD из точки O восстановлен перпендикуляр SO длиной 5. Найдите значение выражения 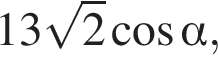 где
где ![]() — линейный угол двугранного угла BSCD, если
— линейный угол двугранного угла BSCD, если 
 и известно, что площадь ABCD равна 80.
и известно, что площадь ABCD равна 80.

 Значит,
Значит, 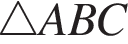 — равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что
— равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что  и
и 
 Значит, длина отрезка
Значит, длина отрезка 
 равна 360°, поэтому
равна 360°, поэтому 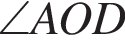 равен 50°. Углы
равен 50°. Углы 

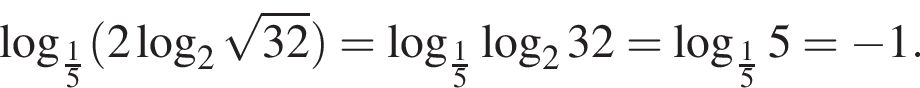
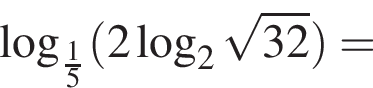
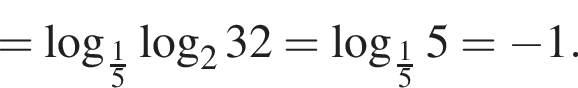
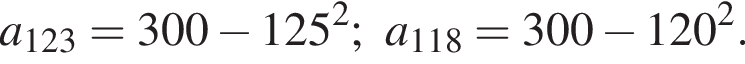 Воспользуемся формулой разности квадратов:
Воспользуемся формулой разности квадратов: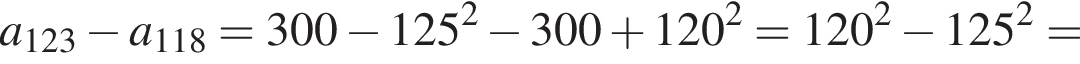
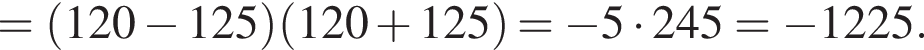
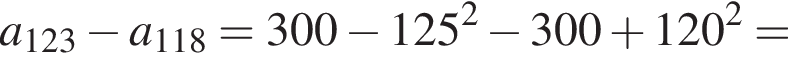
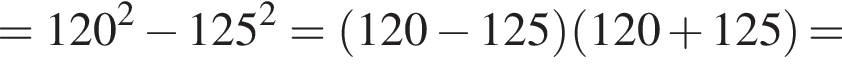
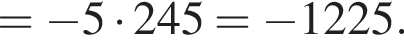
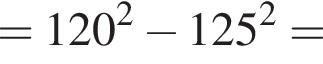
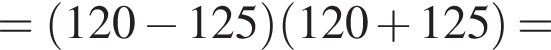
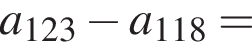
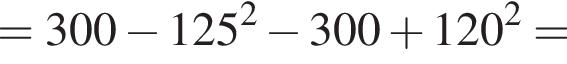
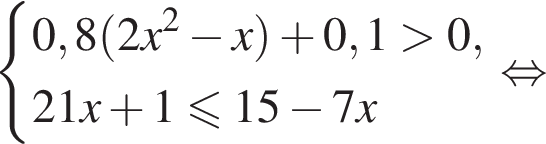
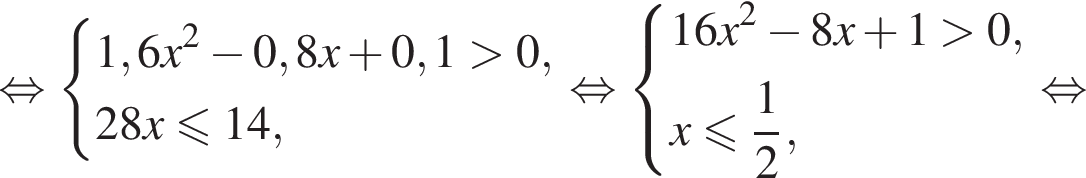
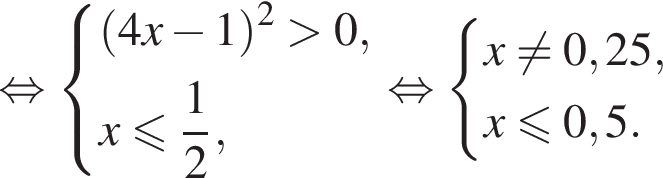
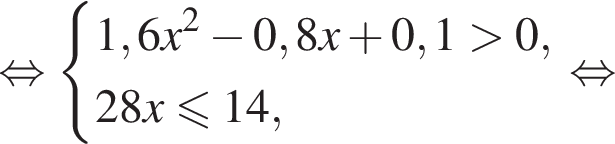
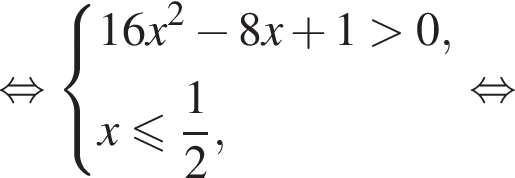
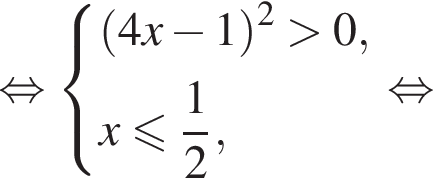
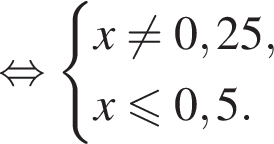

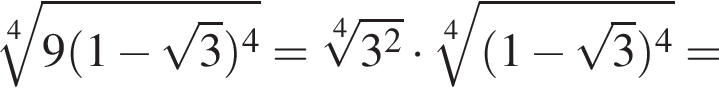
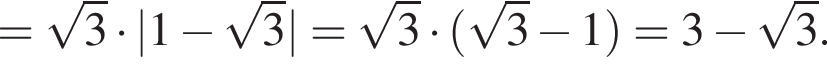
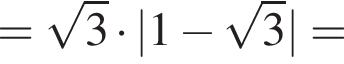
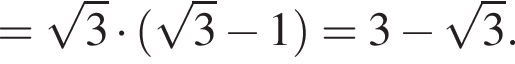
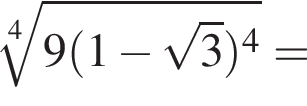
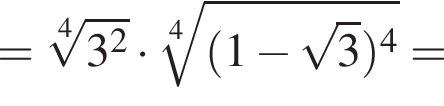
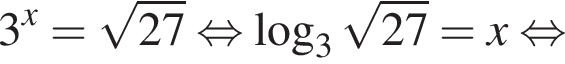
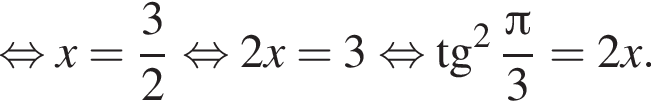
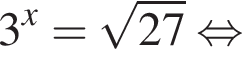
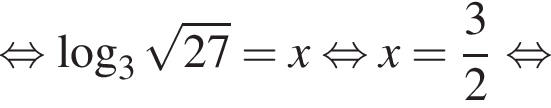

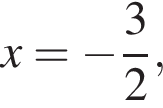 уравнение 2 имеет корень
уравнение 2 имеет корень  уравнение 5 имеет корень
уравнение 5 имеет корень 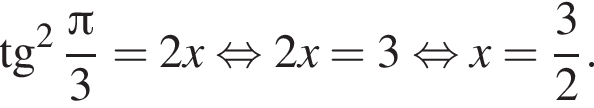

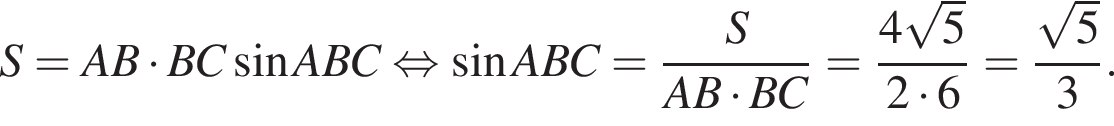

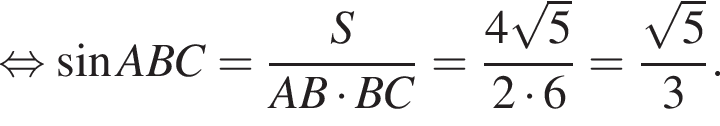
 заметив, что угол ABC тупой:
заметив, что угол ABC тупой: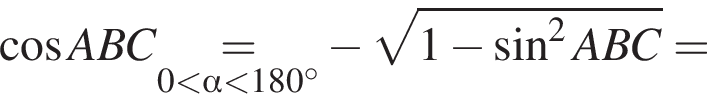
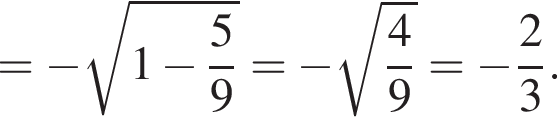
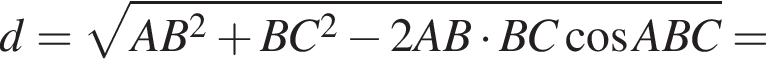
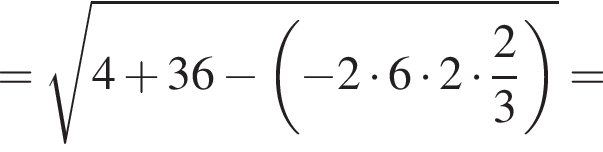


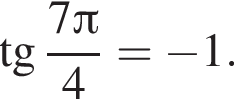 Поэтому:
Поэтому: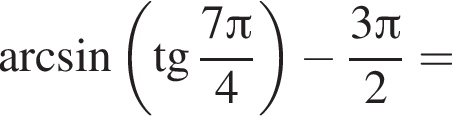
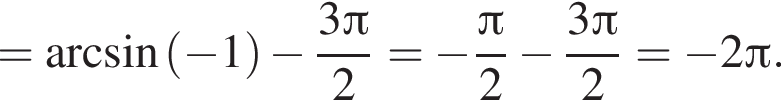
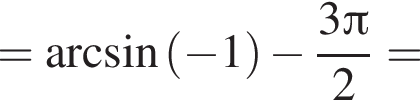
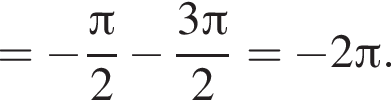
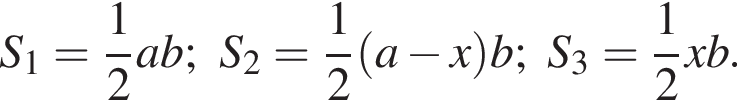
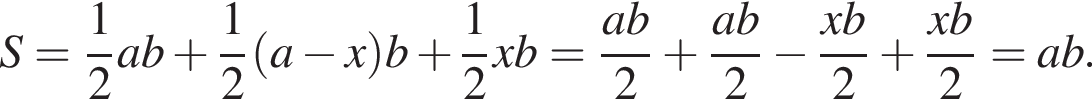
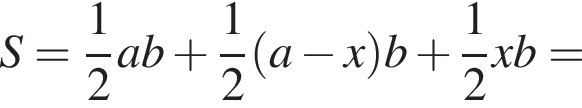
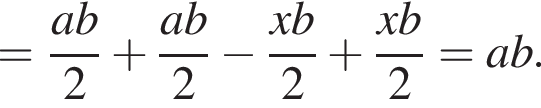
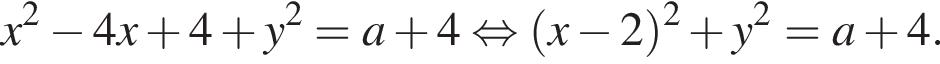
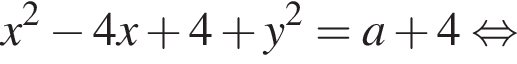

 а радиус — это расстояние от точки A до вершины параболы.
а радиус — это расстояние от точки A до вершины параболы.
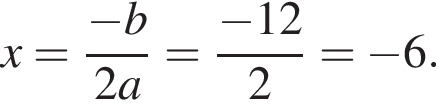 Подставим найденное значение x в изначальное уравнение параболы и получим
Подставим найденное значение x в изначальное уравнение параболы и получим 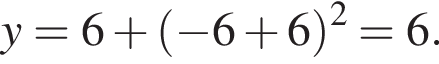 Таким образом, вершина параболы расположена в точке (−6; 6).
Таким образом, вершина параболы расположена в точке (−6; 6).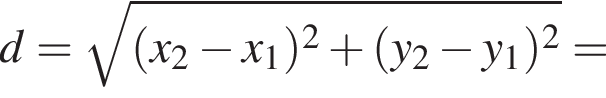
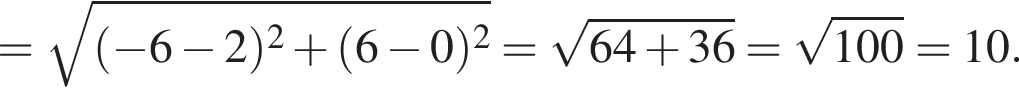
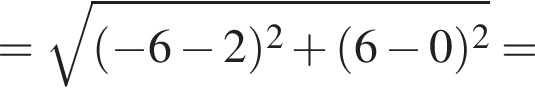


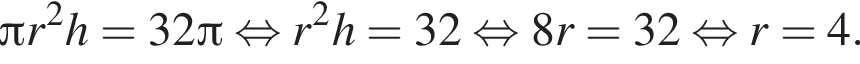

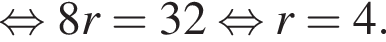
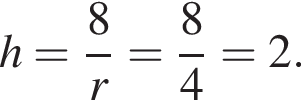
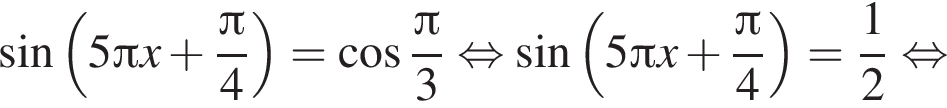
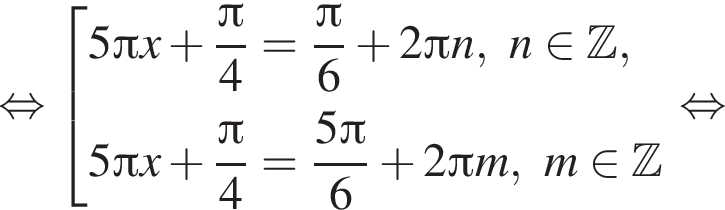
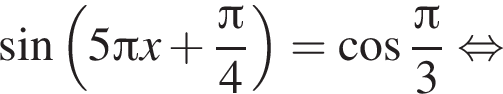
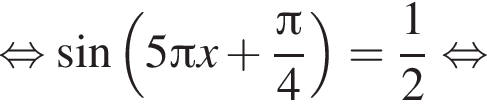
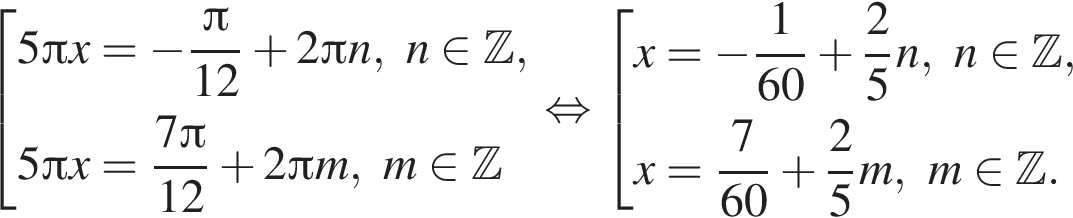
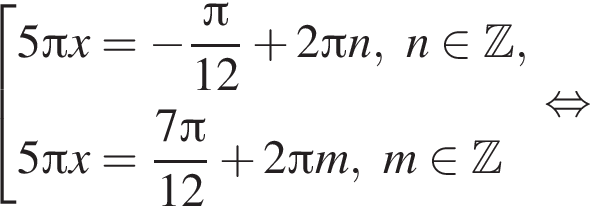
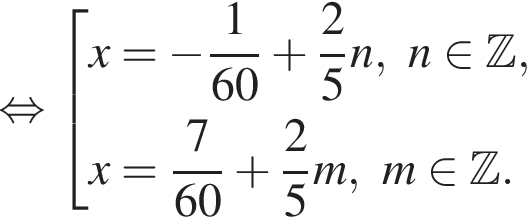
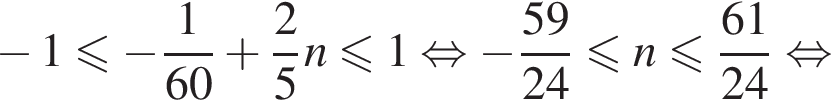
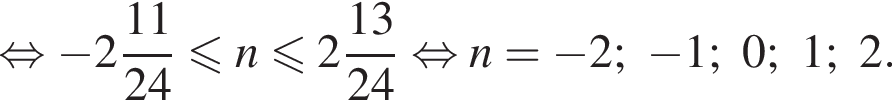
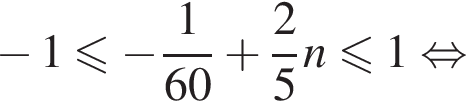
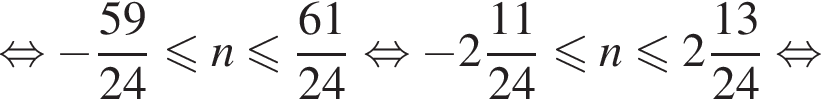

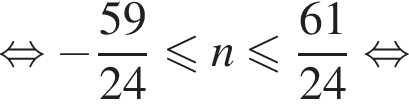
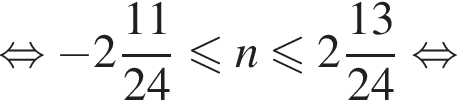
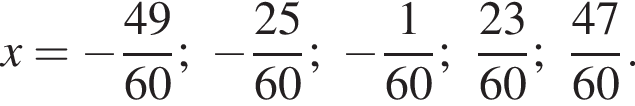
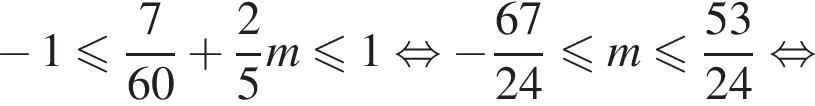
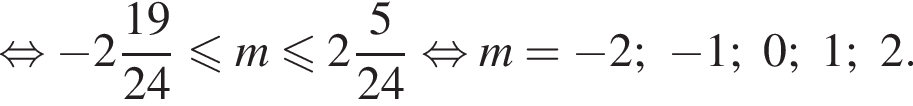

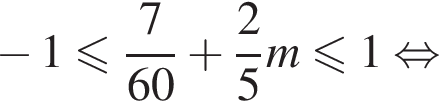
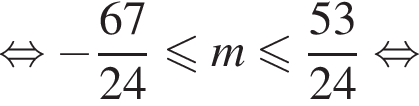
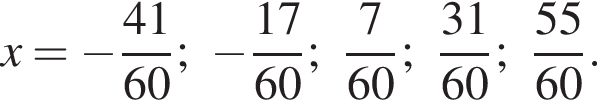
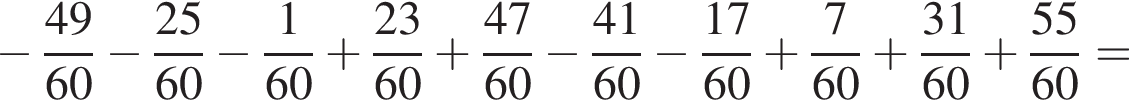
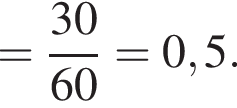
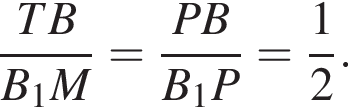
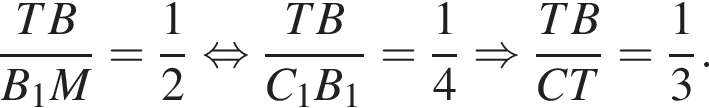
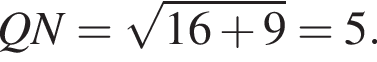
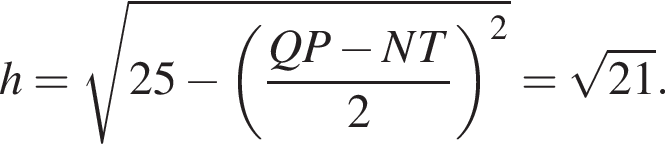


 при
при  значит, ее минимальное значение не может быть равно −16.
значит, ее минимальное значение не может быть равно −16.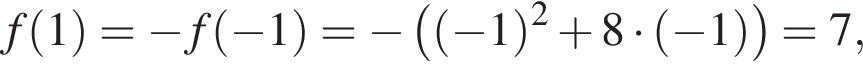
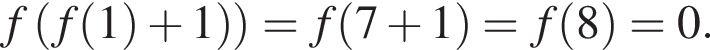 Утверждение 5 верно.
Утверждение 5 верно.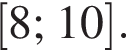 Утверждение 6 неверно.
Утверждение 6 неверно.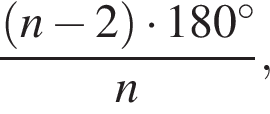 где n количество вершин. Тогда
где n количество вершин. Тогда 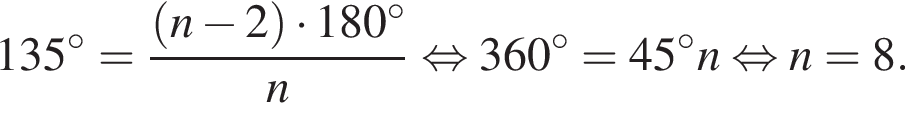
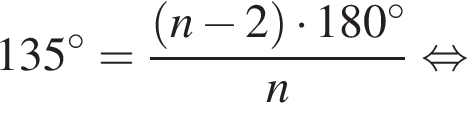
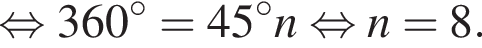
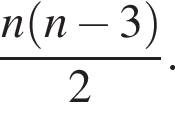 При n = 8, получаем, что диагоналей 20. Второе утверждение верно.
При n = 8, получаем, что диагоналей 20. Второе утверждение верно.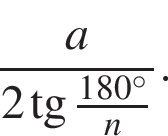
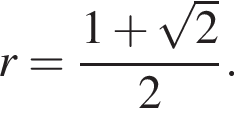 Третье утверждение неверно.
Третье утверждение неверно.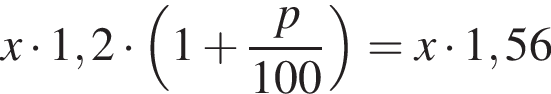
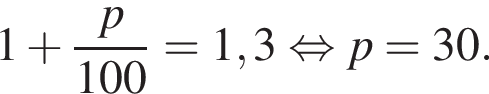
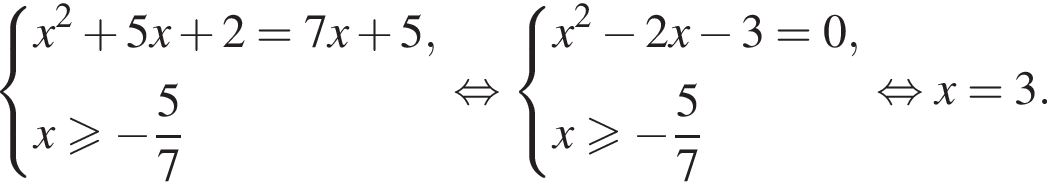
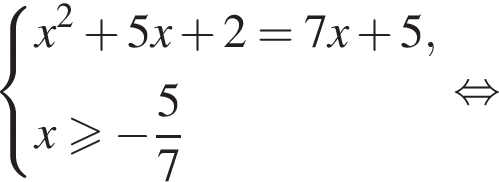
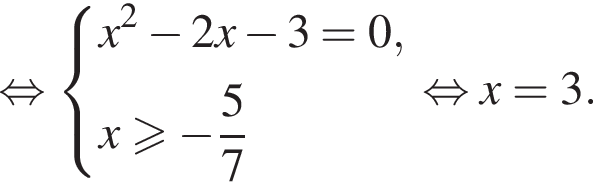
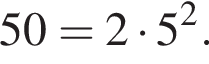
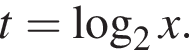
 Имеем:
Имеем: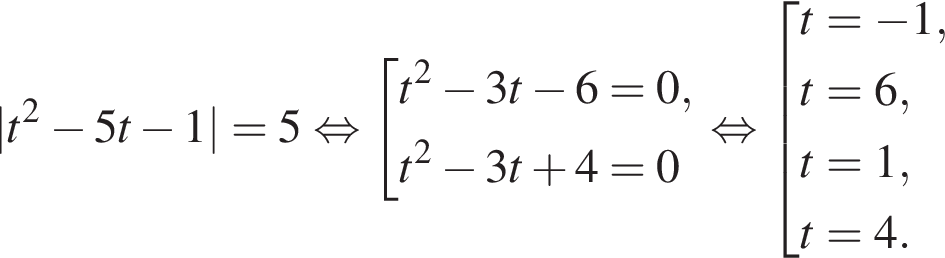
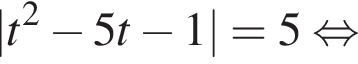
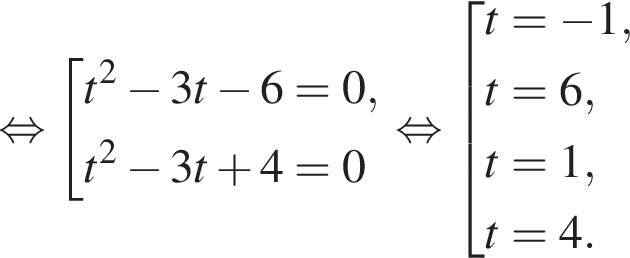
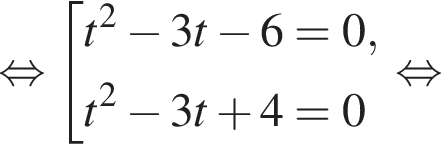
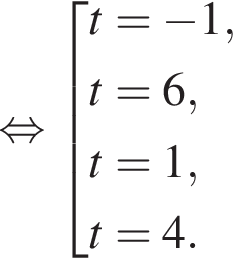
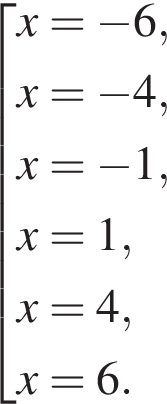

 так как
так как 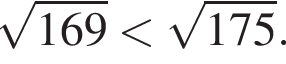 Тогда домножим неравенство на данное число, поменяв знак, и решим его:
Тогда домножим неравенство на данное число, поменяв знак, и решим его: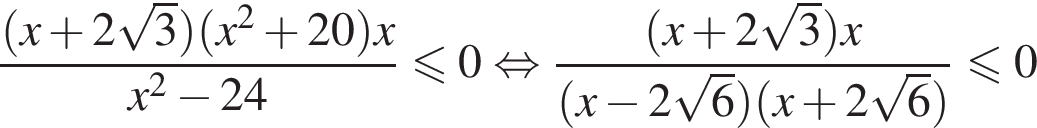
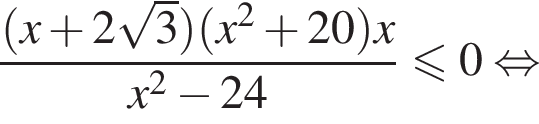
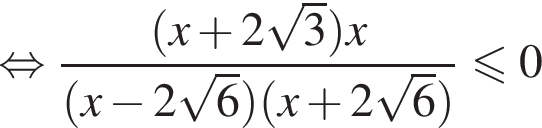

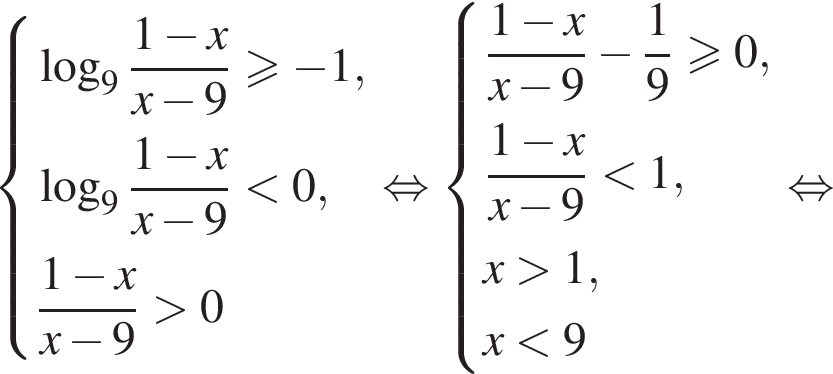
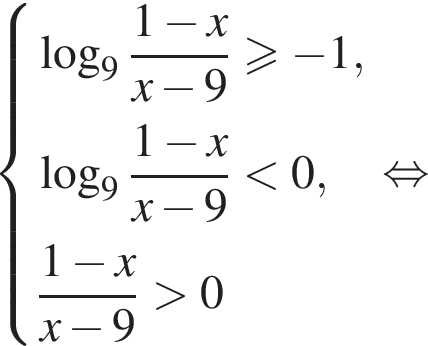
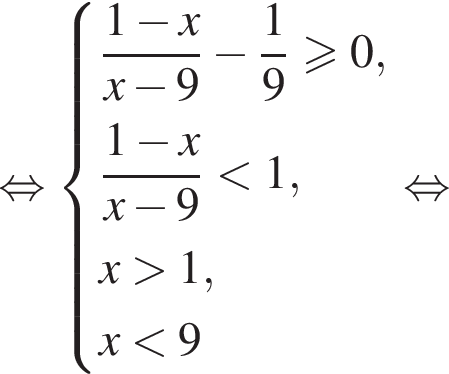
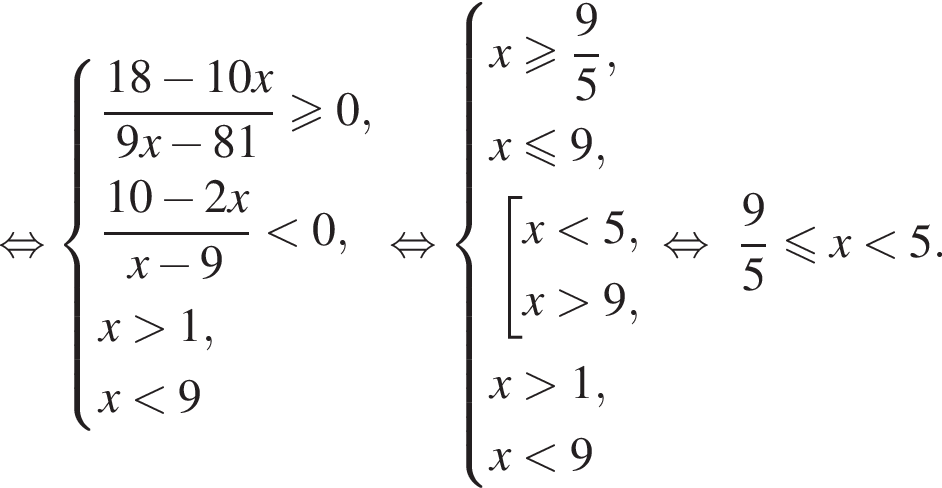
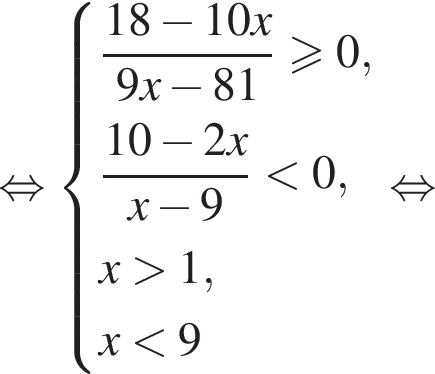
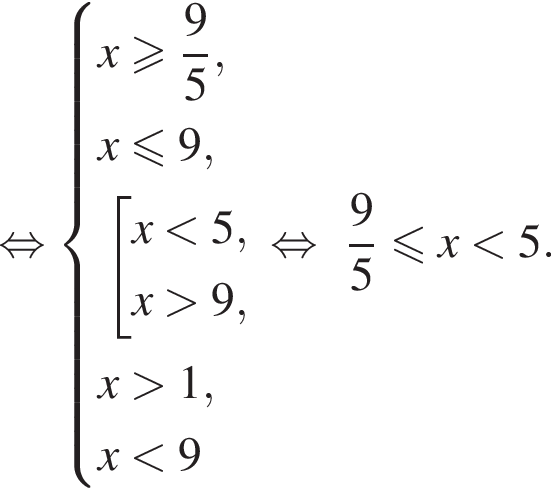
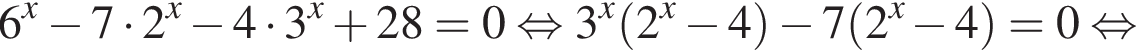
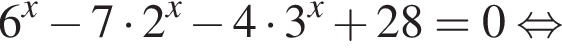
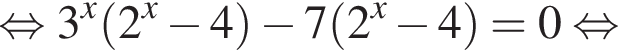
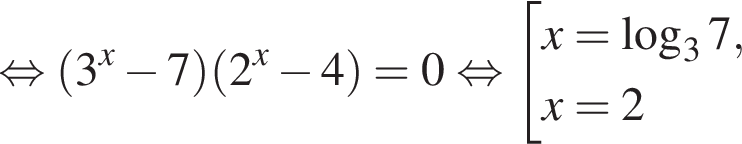
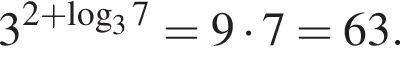
 Из соотношения
Из соотношения 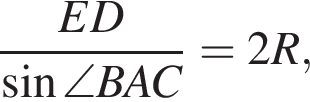
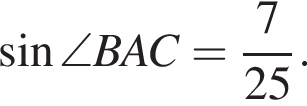
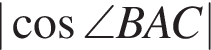 из основного тригонометрического тождества.
из основного тригонометрического тождества.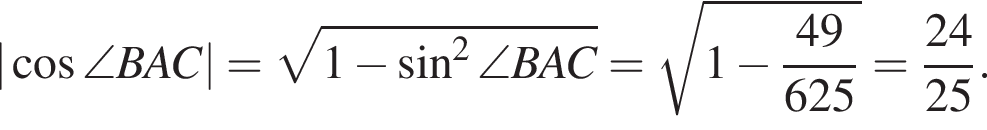
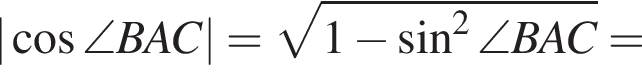
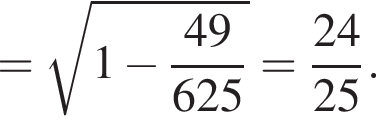
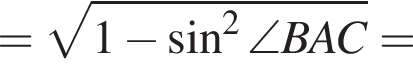
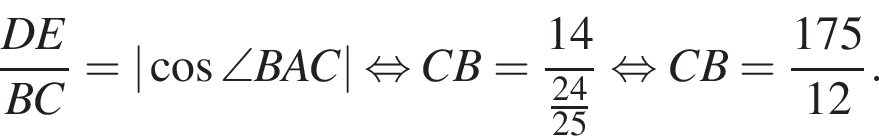
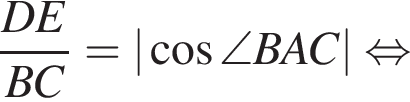
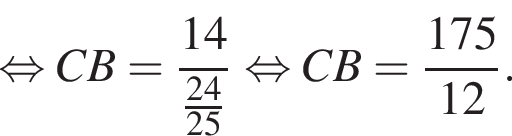
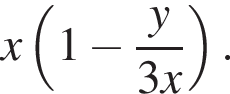 Второй работал
Второй работал 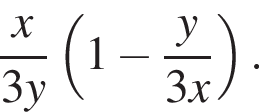 Если оба они выполнили
Если оба они выполнили 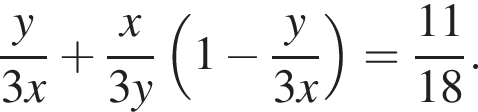 Пусть
Пусть 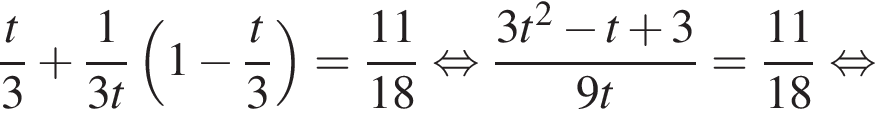
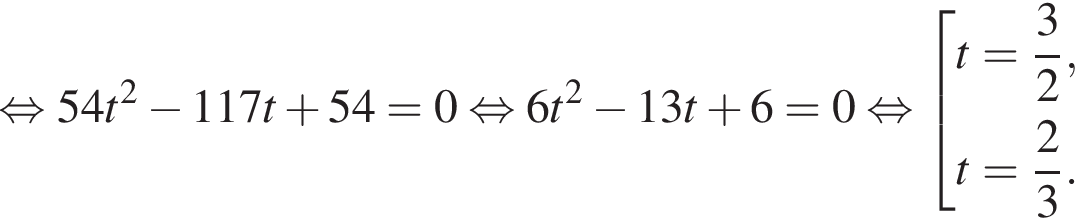

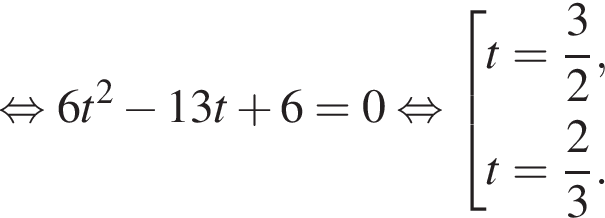
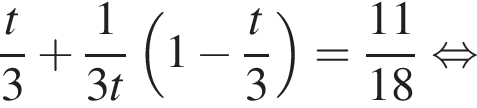
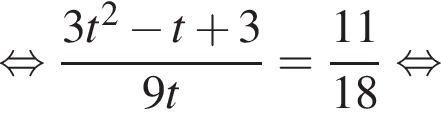
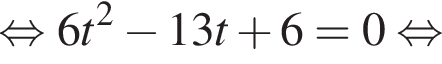
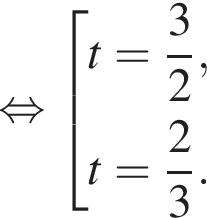
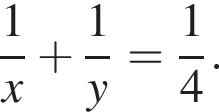 Зная, что
Зная, что 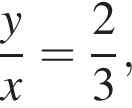 получаем, что
получаем, что 
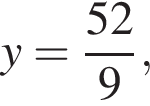 или
или 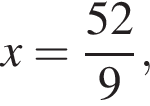
 Таким образом, рабочему с меньшей производительностью потребуется 13 часов.
Таким образом, рабочему с меньшей производительностью потребуется 13 часов.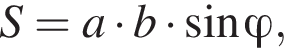 где a и b стороны параллелограмма, а
где a и b стороны параллелограмма, а  а параллелограмм ABCD является прямоугольником. По теореме Пифагора:
а параллелограмм ABCD является прямоугольником. По теореме Пифагора: